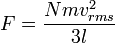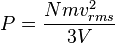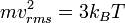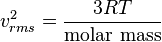Jumat, 16 Juli 2010
KINEMATIKA GERAK LURUS
3 Votes
Quantcast
Persamaan gerak dalam dua dimensi digambarkan menggunakan fungsi dalam vektor, misalnya vektor posisi digambarkan sebagai bagian dari koordinat X dan Y menjadi :
\vec{r} = xi + yj
Jika terdapat dua koordinat masing-masing \vec{r_{1}}= x_{1}i + y_{1}j dan \vec{r_{2}} = x_{2}i + y_{2}j
maka vektor perpindahannya adalah \Delta \vec{r} = (x_{2}-x_{1})i + (y_{2}-y_{1})j atau dapat pula dinyatakan sebagai \Delta \vec{r} = {\Delta x}i + {\Delta y}j
Perlu anda ingat bahwa perpindahan adalah perubahan posisi.
Vektor Kecepatan Rata-Rata
Kecepatan didefinisikan sebagai perubahan posisi setiap satuan waktu, sehingga secara vektor, fungsi kecepatan ini dituliskan sebagai v = \frac {\Delta r}{\Delta t}
maka fungsi kecepatan dapat dituliskan sebagai v = \frac {\Delta x}{\Delta t}i + \frac {\Delta y}{\Delta t}j
karena {\Delta r} = {\Delta x}i + {\Delta y}j
Fungsi di atas hanya digunakan untuk menentukan vektor kecepatan rata-rata
Adapun Fungsi kecepatan sesaat dinyatakan menurut fungsi v = \frac {\delta r}{\delta t} yang dapat pula dituliskan sebagai v = \frac {\delta x}{\delta t}i + \frac {\delta y}{\delta t}j
fungsi \frac {\delta}{\delta t} menyatakan laju perubahan atau diferensial/ turunan
Teori kinetik
Teori kinetik
| . |

Di pertengahan abad ke-19, ilmuwan mengembangkan suatu teori baru untuk menggantikan teori kalorik. Teori ini bedasarkan pada anggapan bahwa zat disusun oleh partikel-partikel sangat kecil yang selalu bergerak. Bunyi teori Kinetik adalah sebagai berikut:
- Dalam benda yang panas, partikel-partikel bergerak lebih cepat dan karena itu memiliki energi yang lebih besar daripada partikel-partikel dalam benda yang lebih dingin.
Teori Kinetik (atau teori kinetik pada gas) berupaya menjelaskan sifat-sifat makroscopik gas, seperti tekanan, suhu, atau volume, dengan memperhatikan komposisi molekular mereka dan gerakannya. Intinya, teori ini menytakan bahwa tekanan tidaklah disebabkan oleh denyut-denyut statis di antara molekul-molekul, seperti yang diduga Isaac Newton, melainkan disebabkan oleh tumbukan antarmolekul yang bergerak pada kecepatan yang berbeda-beda. Teori Kinetik dikenal pula sebagai Teori Kinetik-Molekular atau Teori Tumbukan atau Teori Kinetik pada Gas.
| |
Postulat
Teori untuk gas ideal memiliki asumsi-asumsi berikut ini:
- Gas terdiri dari partikel-partikel sangat kecil, dengan [[massa] tidak nol.
- Banyaknya molekul sangatlah banyak, sehingga perlakuan statistika dapat diterapkan.
- Molekul-molekul ini bergerak secara konstan sekaligus acak. Partikel-partike yang bergerak sangat cepat itu secara konstan bertumbukan dengan dinding-dinding wadah.
- Tumbukan-tumbukan partikel gas terhadap dinding wadah bersifat lenting (elastis) sempurna.
- Interaksi antarmolekul dapat diabaikan (negligible). Mereka tidak mengeluarkan gaya satu sama lain, kecuali saat tumbukan terjadi.
- Keseluruhan volume molekul-molekul gas individual dapat diabaikan bila dibandingkan dengan volume wadah. Ini setara dengan menyatakan bahwa jarak rata-rata antarpartikel gas cukuplah besar bila dibandingkan dengan ukuran mereka.
- Molekul-molekul berbentuk bulat (bola) sempurna, dan bersifat lentur (elastic).
- Energi kinetik rata-rata partikel-partikel gas hanya bergantung kepada suhu sistem.
- Efek-efek relativistik dapat diabaikan.
- Efek-efek Mekanika kuantum dapat diabaikan. Artinya bahwa jarak antarpartikel lebih besar daripada panjang gelombang panas de Broglie dan molekul-molekul dapat diperlakukan sebagai objek klasik.
- Waktu selama terjadinya tumbukan molekul dengan dinding wadah dapat diabaikan karena berbanding lurus terhadap waktu selang antartumbukan.
- Persamaan-persamaan gerak molekul berbanding terbalik terhadap waktu.
Lebih banyak pengembangan menenangkan asumsi-asumsi ini dan didasarkan kepada Persamaan Boltzmann. Ini dapat secara akurat menjelaskan sifat-sifat gas padat, sebab mereka menyertakan volume molekul. Asumsi-asumsi penting adalah ketiadaan efek-efek quantum, kekacauan molekular dan gradien kecil di dalam sifat-sifat banyaknya. Perluasan terhadap orde yang lebih tinggi dalam kepadatan dikenal sebagai perluasan virial. Karya definitif adalah buku tulisan Chapman dan Enskog, tetepi terdapat pengembangan yang lebih modern dan terdapat pendekatan alternatif yang dikembangkan oleh Grad, didasarkan pada perluasan momentum.[rujukan?] Di dalam batasan lainnya, untuk gas yang diperjarang, gradien-gradien di dalam sifat-sifat besarnya tidaklah kecil bila dibandingkan dengan lintasan-lintasan bebas rata-ratanya. Ini dikenal sebagai rezim Knudsen regime dan perluasan-perluasannya dapat dinyatakan dengan Bilangan Knudsen.
Teori Kinetik juga telah diperluas untuk memasukkan tumbukan tidak lenting di dalam materi butiran oleh Jenkins dan kawan-kawan.[rujukan?]
Tekanan
Tekanan dijelaskan oleh teori kinetik sebagai kemunculan dari gaya yang dihasilkan oleh molekul-molekul gas yang menabrak dinding wadah. Misalkan suatu gas denagn N molekul, masing-masing bermassa m, terisolasi di dalam wadah yang mirip kubus bervolume V. Ketika sebuah molekul gas menumbuk dinding wadah yang tegak lurus terhadap sumbu koordinat x dan memantul dengan arah berlawanan pada laju yang sama (suatu tumbukan lenting), maka momentum yang dilepaskan oleh partikel dan diraih oleh dinding adalah:
di mana vx adalah komponen-x dari kecepatan awal partikel.
Partikel memberi tumbukan kepada dinding sekali setiap 2l/vx satuan waktu (di mana l adalah panjang wadah). Kendati partikel menumbuk sebuah dinding sekali setiap 1l/vx satuan waktu, hanya perubahan momentum pada dinding yang dianggap, sehingga partikel menghasilkan perubahan momentum pada dinding tertentu sekali setiap 2l/vx satuan waktu.
gaya yang dimunculkan partikel ini adalah:
Keseluruhan gaya yang menumbuk dinding adalah:
di mana hasil jumlahnya adalah semua molekul gas di dalam wadah.
Besaran kecepatan untuk tiap-tiap partikel mengikuti persamaan ini:
Kini perhatikan gaya keseluruhan yang menumbuk keenam-enam dinding, dengan menambahkan sumbangan dari tiap-tiap arah, kita punya:
di mana faktor dua muncul sejak saat ini, dengan memperhatikan kedua-dua dinding menurut arah yang diberikan.
Misalkan ada sejumlah besar partikel yang bergerak cukup acak, gaay pada tiap-tiap dinding akan hampir sama dan kini perhatikanlah gaya pada satu dinding saja, kita punya:
Kuantitas  dapat dituliskan sebagai
dapat dituliskan sebagai 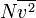 , di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan
, di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan  di mana vrms dalah akar kuadrat rata-rata kecepatan semua partikel.
di mana vrms dalah akar kuadrat rata-rata kecepatan semua partikel.
Jadi, gaya dapat dituliskan sebagai:
Tekanan, yakni gaya per satuan luas, dari gas dapat dituliskan sebagai:
di mana A adalah luas dinding sasaran gaya.
Jadi, karena luas bagian yang berseberangan dikali dengan panjang sama dengan volume, kita punya pernyataan berikut untuk tekanan
di mana V adalah volume. Maka kita punya
Karena Nm adalah masa keseluruhan gas, maka kepadatan adalah massa dibagi oleh volume 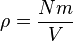 .
.
Maka tekanan adalah
Hasil ini menarik dan penting, sebab ia menghubungkan tekanan, sifat makroskopik, terhadap energi kinetik translasional rata-rata per molekul  yakni suatu sifat mikroskopik. Ketahuilah bahwa hasil kali tekanan dan volume adalah sepertiga dari keseluruhan energi kinetik Suhu dan energi kinetik
yakni suatu sifat mikroskopik. Ketahuilah bahwa hasil kali tekanan dan volume adalah sepertiga dari keseluruhan energi kinetik Suhu dan energi kinetik
Dari hukum gas ideal
-
- PV = NkBT(1)
dimana B adalah konstanta Boltzmann dan T adalah suhu absolut. Dan dari rumus diatas, dihasilkan Gagal memparse (kesalahan sintaks): PV={Nmv_{rms}^2\overset 3}
Derivat:
-

 (2)
(2)
yang menuju ke fungsi energi kinetik dari sebuah molekul
Energi kinetik dari sistem adalah N kali lipat dari molekul 
Suhunya menjadi
-
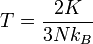 (3)
(3)
Persamaan 3 ini adalah salah satu hasil penting dari teori kinetik
| “ | Rerata energi kinetik molekuler adalah sebanding dengan suhu absolut. | ” |
Dari persamaan 1 dan 3 didapat:
-
 (4)
(4)
Dengan demikian, hasil dari tekanan dan volume tiap mol sebanding dengan rerata energi kinetik molekuler. Persamaan 1 dan 4 disebut dengan hasil klasik, yang juga dapat diturunkan dari mekanika statistik[1].
Karena 3N adalah derajat kebebasan (DK) dalam sebuah sistem gas monoatomik dengan N partikel, energi kinetik tiap DK adalah:
-
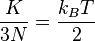 (5)
(5)
Dalam energi kinetik tiap DK, konstanta kesetaraan suhu adalah setengah dari konstanta Boltzmann. Hasil ini berhubungan dengan teorema ekuipartisi. Seperti yang dijelaskan pada artikel kapasitas bahang, gas diatomik seharusnya mempunyai 7 derajat kebebasan, tetapi gas yang lebih ringan berlaku sebagai gas yang hanya mempunyai 5. Dengan demikian, energi kinetik tiap kelvin (gas ideal monoatomik) adalah:
- Tiap mole: 12.47 J
- Tiap molekul: 20.7 yJ = 129 μeV
Pada STP (273,15 K , 1 atm), didapat:
- Tiap mole: 3406 J
- Tiap molekul: 5.65 zJ = 35.2 meV
Banyaknya tumbukan dengan dinding
Jumlah tumbukan atom dengan dinding wadah tiap satuan luar tiap satuan waktu dapat diketahui. Asumsikan pada gas ideal, derivasi dari [2] menghasilkan persamaan untuk jumlah seluruh tumbukan tiap satuan waktu tiap satuan luas:
Laju RMS molekul
Dari persamaan energi kinetik dapat ditunjukkan bahwa:
dengan v pada m/s, T pada kelvin, dan R adalah konstanta gas. Massa molar diberikan sebagai kg/mol. Kelajuan paling mungkin adalah 81.6% dari kelajuan RMS, dan rerata kelajuannya 92.1% (distribusi kelajuan Maxwell-Boltzmann).
Banyaknya tumbukan dengan dinding
One can calculate the number of atomic or molecular collisions with a wall of a container per unit area per unit time.
Assuming an ideal gas, a derivation[3] results in an equation for total number of collisions per unit time per area:
Laju RMS molekul
From the kinetic energy formula it can be shown that
hukum archimedes
Mengapa Hukum Archimedes menjadi sebuah penemuan besar?
 Mengapa merupakan salah satu penemuan terbesar ?
Mengapa merupakan salah satu penemuan terbesar ? Sejarah Penemuan
Sejarah PenemuanTahun 260BC, Archimedes yang waktu itu masih berusia 26 tahun sedang mempelajari ilmu astronomi dan geometry di Syracuse, Sicilia. Suatu hari Archimedes tertarik dengan permainan 4 bocah di pantai dengan sebuah papan kayu yang mengapung. Mereka mencoba menyeimbangkan papan tersebut di atas batu karang setinggi pinggang. Salah seorang anak berdiri pada ujung papan, kemudian 3 teman lainnya meloncat ke ujung yang lainnya. Bocah yang sendirian itu kemudian terlempar ke atas.
Kemudian anak-anak ini menggeser papannya supaya hanya seperempat bagian pendek. Ketiga bocah itu menaiki bagian yang pendek di ujungnya. Anak yang keempat segera meloncat ke bagian yang panjang yang posisinya naik ke atas, yang efeknya langsung melempar teman-temannya ke udara.Archimedes sangat terpesona. Dia kemudian bertekad untuk memahami prinsip ini supaya benda yang ringan (seorang laki-laki) mampu mengangkat benda berat (tiga laki-laki).
Archimedes menggunakan selembar papan dan sebuah balok kayu kecil untuk memodelkan anak laki-laki dan papan pengapung mereka. Dia membuat balok segitiga untuk memodelkan batu karang mereka. Dengan menghitung sambil menyeimbangkan berbagai kombinasi berat pada ujung pengdongkrak, Archimedes menyadari bahwa pengungkit ini merupakan salah satu contoh dari hasil kerja Euclid. Gaya yang mendorong ke bawah setiap ujung pada pengungkit harus proposional dengan panjang papan pada setiap sisi terhadap titik penyeimbang. Dia menemukan konsep matematika dari pengungkit, suatu sistem pengangkutan yang paling umum dan dasar yang pernah dirumuskan.
Lima belas tahun kemudian pada tahun 245BC, Archimedes diperintahkan Raja Hieron untuk mencari tahu apakah ahli emas telah menipu raja. Hieron memberi sebongkah emas kepada ahli emas untuk dijadikan mahkota berbahan emas. Walaupun mahkota ini beratnya sama dengan emas asli, raja curiga jika ahli emas ini melapisi logam yang lebih murah didalamnya dengan emas. Archimedes diperintahkan untuk mencari tahu apakah mahkota ini murni emas tanpa harus merusak mahkota itu sendiri.
Sepertinya ini merupakan pekerjaan yang mustahil. Ketika sedang mandi di tempat permandian umum, Archimedes menyadari lengannya terapung diatas air. Sebuah ide kemudian terbesit di benaknya. Dia menarik tangannya kedalam air dan dia merenggangkan lengannya. Lengannya dengan sendiri mengapung kembali ke atas. Kemudian dia mencoba berdiri dari bak, level air menjadi menyusut, kemudian dia duduk kembali, level air meningkat kembali. Dia berbaring, air naik lebih tinggi lagi, dan dia merasa lebih ringan. Dia berdiri, level air menurun dan dia merasa dirinya lebih berat. Air harusnya telah mendorong dia keatas sehingga dia merasa ringan.
Dia kemudian mengambil sebuah batu dan sebalok kayu yang memiliki ukuran sama ke dalam bak dan merendamkan mereka kedua-duanya. Batu tenggelam tetapi terasa ringan. Dia harus menekan kayu supaya tenggelam. Itu artinya air harus menekan ke atas dengan gaya yang relatif terhadap jumlah air yang tergantikan oleh ukuran objek daripada berat dari objek. Seberat apa objek itu dirasakan di air mempengaruhi kepadatan objek.Ini membuat Archimedes mengerti bagaimana memecahkan masalah raja. Dia kembali ke raja. Kuncinya adalah kepadatan. Jika mahkota ini terbuat dari logam bukan emas, dia dapat memiliki berat yang sama tetapi akan memiliki kepadatan yang berbeda sehingga akan menumpahkan jumlah air yang berbeda.
Mahkota dan sebuah emas yang beratnya sama di masukkan ke sebuah mangkok berisi air. Mahkotanya ternyata menumpahkan air lebih banyak sehingga terbukti mahkota itu adalah palsu. Lebih penting, Archimedes kemudian menemukan prinsip pengapungan: Air menekan ke atas sebuah objek dengan gaya yang setara dengan jumlah air yang ditumpahkannya.
JANGKA SORONG
JANGKA SORONG
Jangka sorong adalah suatu alat ukur panjang yang dapat dipergunakan untuk mengukur panjang suatu benda dengan ketelitian hingga 0,1 mm. keuntungan penggunaan jangka sorong adalah dapat dipergunakan untuk mengukur diameter sebuah kelereng, diameter dalam sebuah tabung atau cincin, maupun kedalam sebuah tabung.
Pada gambar disamping ditunjukkan bagian-bagian dari jangka sorong. (sorot masing-masing bagian dari jangka sorong tersebut untuk mengetahui nama setiap bagian).
Secara umum, jangka sorong terdiri atas 2 bagian yaitu rahang tetap dan rahang geser. Jangka sorong juga terdiri atas 2 bagian yaitu skala utama yang terdapat pada rahang tetap dan skala nonius (vernier) yang terdapat pada rahang geser.
Sepuluh skala utama memiliki panjang 1 cm, dengan kata lain jarak 2 skala utama yang saling berdekatan adalah 0,1 cm. Sedangkan sepuluh skala nonius memiliki panjang 0,9 cm, dengan kata lain jarak 2 skala nonius yang saling berdekatan adalah 0,09 cm. Jadi beda satu skala utama dengan satu skala nonius adalah 0,1 cm – 0,09 cm = 0,01 cm atau 0,1 mm. Sehingga skala terkecil dari jangka sorong adalah 0,1 mm atau 0,01 cm.
Ketelitian dari jangka sorong adalah setengah dari skala terkecil. Jadi ketelitian jangka sorong adalah : Dx = ½ x 0,01 cm = 0,005 cm
Dengan ketelitian 0,005 cm, maka jangka sorong dapat dipergunakan untuk mengukur diameter sebuah kelereng atau cincin dengan lebih teliti (akurat).
Seperti yang sudah dijelaskan sebelumnya bahwa jangka sorong dapat dipergunakan untuk mengukur diameter luar sebuah kelereng, diameter dalam sebuah tabung atau cincin maupun untuk mengukur kedalaman sebuah tabung. Berikut akan dijelaskan langkah-langkah menggunakan jangka sorong untuk keperluan tersebut
1. Mengukur diameter luar
Untuk mengukur diameter luar sebuah benda (misalnya kelereng) dapat dilakukan dengan langkah sebagai berikut
* Geserlah rahang geser jangka sorong kekanan sehingga benda yang diukur dapat masuk diantara kedua rahang (antara rahang geser dan rahang tetap)
* Letakkan benda yang akan diukur diantara kedua rahang.
* Geserlah rahang geser kekiri sedemikian sehingga benda yang diukur terjepit oleh kedua rahang
* Catatlah hasil pengukuran anda
2. Mengukur diameter dalam
Untuk mengukur diameter dalam sebuah benda (misalnya diameter dalam sebuah cincin) dapat dilakukan dengan langkah sebagai berikut :
* Geserlah rahang geser jangka sorong sedikit kekanan.
* Letakkan benda/cincin yang akan diukur sedemikian sehingga kedua rahang jangka sorong masuk ke dalam benda/cincin tersebut
* Geserlah rahang geser kekanan sedemikian sehingga kedua rahang jangka sorong menyentuh kedua dinding dalam benda/cincin yang diukur
* Catatlah hasil pengukuran anda
3. Mengukur kedalaman
Untuk mengukur kedalaman sebuah benda/tabung dapat dilakukan dengan langkah sebagai berikut :
* Letakkan tabung yang akan diukur dalam posisi berdiri tegak.
* Putar jangka (posisi tegak) kemudian letakkan ujung jangka sorong ke permukaan tabung yang akan diukur dalamnya.
* Geserlah rahang geser kebawah sehingga ujung batang pada jangka sorong menyentuh dasar tabung.
* Catatlah hasil pengukuran anda.
Untuk membaca hasil pengukuran menggunakan jangka sorong dapat dilakukan dengan langkah sebagai berikut :
1. Bacalah skala utama yang berimpit atau skala terdekat tepat didepan titik nol skala nonis.
2. Bacalah skala nonius yang tepat berimpit dengan skala utama.
3. Hasil pengukuran dinyatakan dengan persamaan :
Hasil = Skala Utama + (skala nonius yang berimpit x skala terkecil jangka sorong) = Skala Utama + (skala nonius yang berimpit x 0,01 cm)
Karena Dx = 0,005 cm (tiga desimal), maka hasil pembacaan pengukuran (xo) harus juga dinyatakan dalam 3 desimal. Tidak seperti mistar, pada jangka sorong yang memiliki skala nonius, Anda tidak pernah menaksir angka terakhir (desimal ke-3) sehingga anda cukup berikan nilai 0 untuk desimal ke-3. sehingga hasil pengukuran menggunakan jangka sorong dapat anda laporkan sebagai :
Panjang L = xo + Dx
Misalnya L = (4,990 + 0,005) cm
Jangka sorong biasanya digunakan untuk:
1. mengukur suatu benda dari sisi luar dengan cara diapit;
2. Mengukur sisi dalam suatu benda yang biasanya berupa lubang (pada pipa, maupun lainnya) dengan cara diulur;
3. Mengukur kedalamanan celah/lubang pada suatu benda dengan cara “menancapkan/menusukkan” bagian pengukur.
4. Jangka sorong memiliki dua macam skala: skala utama dan nonius.
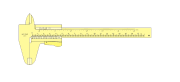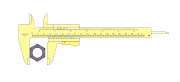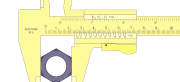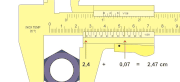
Lihat contoh cara mengukur di bawah.
Lihatlah skala nonius yang berhimpit dengan skala utama. Di contoh, yang berhimpit adalah angka 4 (diberi tanda merah). Itu berarti 0.04 mm. Sekarang lihatlah ke skala utama di sebelah kiri angka nonius 0. Di situ menunjukkan angka 4,7 cm. Berarti hasil pengukurannya adalah 4,7 cm + 0.04 cm = 4,74 cm. Ingat lagi kan pelajaran SMA? Hehe. Untuk pembacaan ke inch prinsipnya sama, hanya saja harus pintar menggunakan skala yang berbeda
jangka sorong
Jangka sorong adalah alat ukur yang ketelitiannya dapat mencapai seperseratus milimeter. Terdiri dari dua bagian, bagian diam dan bagian bergerak. Pembacaan hasil pengukuran sangat bergantung pada keahlian dan ketelitian pengguna maupun alat. Sebagian keluaran terbaru sudah dilengkapi dengan display digital. Pada versi analog, umumnya tingkat ketelitian adalah 0.05mm untuk jangka sorang dibawah 30cm dan 0.01 untuk yang diatas 30cm.
Kegunaan
Kegunaan jangka sorong adalah:
- untuk mengukur suatu benda dari sisi luar dengan cara diapit;
- untuk mengukur sisi dalam suatu benda yang biasanya berupa lubang (pada pipa, maupun lainnya) dengan cara diulur;
- untuk mengukur kedalamanan celah/lubang pada suatu benda dengan cara "menancapkan/menusukkan" bagian pengukur. Bagian pengukur tidak terlihat pada gambar karena berada di sisi pemegang.
Jenis
Gelombang
Gelombang
Pengertian Gelombang
Gelombang adalah bentuk dari getaran yang merambat pada suatu medium. Pada gelombang yang merambat adalah gelombangnya, bukan zat medium perantaranya. Satu gelombang dapat dilihat panjangnya dengan menghitung jarak antara lembah dan bukit (gelombang tranversal) atau menhitung jarak antara satu rapatan dengan satu renggangan (gelombang longitudinal). Cepat rambat gelombang adalah jarak yang ditempuh oleh gelombang dalam waktu satu detik.
Jenis-Jenis Gelombang
1. Gelombang transversal
Gelombang transversal adalah gelombang yang arah rambatannya tegak lurus dengan arah rambatannya. Satu gelombang terdiri atas satu lembah dan satu bukit, misalnya seperti riak gelombang air, benang yang digetarkan, dsb.
2. Gelombang longitudinal
Gelombang longitudinal adalah gelombang yang merambat dalam arah yang berimpitan dengan arah getaran pada tiap bagian yang ada. Gelombang yang terjadi berupa rapatan dan renggangan. Contoh gelombang longitudinal seperti slingki / pegas yang ditarik ke samping lalu dilepas.
Istilah Dalam Gelombang Laut
Gelombang adalah getaran yang merambat. Di dalam perambatannya tidak diikuti oleh berpindahnya partikel-partikel perantaranya. Pada hakekatnya gelombang merupakan rambatan energi (energi getaran).
Macam-macam gelombang
Menurut arah getarnya:
· Gelombang transversal adalah gelombang yang arah getarnya tegak lurus terhadap arah rambatannya. Contoh: gelombang pada tali , gelombang permukaan air, gelobang cahaya, dll.
· Gelombang longitudinal adalah gelombang yang arah getarnya sejajar atau berimpit dengan arah rambatannya. Contoh: gelombang bunyi dan gelombang pada pegas.
Menurut amplitudo dan fasenya :
· Gelombang berjalan adalah gelombang yang amplitudo dan fasenya sama di setiap titik yang dilalui gelombng.
· Gelombng diam (stasioner) adalah gelombang yang amplitudo dan fasenya berubah (tidak sama) di setiap titik yang dilalui gelombang.
Menurut medium perantaranya:
· Gelombang mekanik adalah gelombang yang didalam perambatannya memerlukan medium perantara. Hampir semua gelombang merupakan gelombang mekanik.
· Gelombang elektromagnetik adalah gelombang yang didalam perambatannya tidak memerlukan medium perantara. Contoh : sinar gamma (γ), sinar X, sinar ultra violet, cahaya tampak, infra merah, gelombang radar, gelombang TV, gelombang radio.
Persamaan umum gelombang
Besaran-besaran dalam gelombang hampir sama dengan besaran-besaran yang dimiliki oleh getaran, antara lain, periode, frekuensi, kecepatan, fase, amplitudo.
![]() Gelombang Stasioner (diam)
Gelombang Stasioner (diam)
Gelombang stasioner ini dapat terjadi oleh karena interferensi (penggabungan dua gelombang yaitu gelombang datang dan pantul).
Pantulan gelombang yang terjadi dapat berupa pantulan dengan ujung tetap dan dapat juga pantul pantul merupakan kelanjutan dari gelombang datang (fasenya tetap), tetapi jika pantulan itu terjadi pada ujung tetap, maka gelombang pantul mengalami pembalikan fase (berbeda fase 1800) terhadap gelombang dating.
Penyebab terjadi gelombang laut dipengaruhi beberapa factor berikut:
- Kecepatan angin
- Lama angina bertiup dan luas daerah yang terkena pengaruh
- Kedalaman air laut
- Adanya getaran kulit bumi di dasar laut
- Tetapi factor utamanya karena angin dan gempa
Ombak karena angina = biasanya ombak terjadi karena geseran angina dipermukaan air, sebab itu arah gelombang searah dengan arah angina yang menimbulkannya. Tinggi dan besarnya ombak tergantung kekuatan angiin, semakin kencang anginnya semakin tinngi ombaknya.
Ombak Karena Gempa Laut
Sejarah Tsunami di Indonesia
Tsunami adalah istilah dalam bahasa Jepang yang pada dasarnya menyatakan suatu gelombang laut yang terjadi akibat gempa bumi tektonik di dasar laut. Magnitudo Tsunami yang terjadi di Indonesia berkisar antara 1,5-4,5 skala Imamura, dengan tinggi gelombang Tsunami maksimum yang mencapai pantai berkisar antara 4 - 24 meter dan jangkauan gelombang ke daratan berkisar antara 50 sampai 200 meter dari garis pantai.
Berdasarkan Katalog gempa (1629 - 2002) di Indonesia pernah terjadi Tsunami sebanyak 109 kali , yakni 1 kali akibat longsoran (landslide), 9 kali akibat gunung berapi dan 98 kali akibat gempabumi tektonik.
Yang paling mungkin dapat menimbulkan tsunami adalah : gempa yang terjadi di dasarkan laut, kedalaman pusat gempa kurang dari 60 km, magnitudo gempa lebih besar dari 6,0 skala Richter, serta jenis pensesaran gempa tergolong besar naik atau sesar turun. Hal diatas yang memicu terjadinya tsunami di daerah Kepulauan Seram,
Gerak Harmonik Sederhana
Gerak Harmonik Sederhana
 Pengantar
Pengantar
Dalam kehidupan sehari-hari terdapat banyak benda yang bergetar. Senar gitar yang sering anda main atau dimainkan oleh gitaris group band musik terkenal yang kadang membuat anda menjerit histeris bahkan sampai menangis tersedu-sedu, getaran garpu tala, getaran mobil ketika mesinnya dinyalakan atau ketika mobil mencium mobil lainnya hingga penumpangnya babak belur. Ingat juga ketika anda tertawa terpingkal-pingkal tubuh anda juga bergetar, demikian juga rumah anda yang bergetar dasyat hingga ambruk ketika terjadi gempa bumi. Sangat banyak contoh getaran dalam kehidupan kita, sehingga jika disebutkan satu persatu maka tentu sangat melelahkan. Silahkan dipikirkan sendiri contoh lainnya.
Getaran dan gelombang merupakan dua hal yang saling berkaitan. Gelombang, baik itu gelombang air laut, gelombang gempa bumi, gelombang suara yang merambat di udara; semuanya bersumber pada getaran. Dengan kata lain, getaran adalah penyebab adanya gelombang. Mengenai gelombang, selengkapnya akankita pelajari pada pokok bahasan tersendiri. Sekarang terlebih dahulu kita pelajari pokok bahasan getaran. Semoga setelah mempelajari getaran, dirimu tidak ikut bergetar, apalagi ketika gurumu menyajikan soal-soal hitungan yang membuat dirimu mabuk kepayang.
Setiap gerak yang terjadi secara berulang dalam selang waktu yang sama disebut gerak periodik. Karena gerak ini terjadi secara teratur maka disebutjuga sebagai gerak harmonik/harmonis. Apabila suatu partikel melakukan gerak periodik pada lintasan yang sama maka geraknya disebut gerak osilasi/getaran. Bentuk yang sederhana dari gerak periodik adalah benda yang berosilasi pada ujung pegas. Karenanyakita menyebutnya gerak harmonis sederhana. Banyak jenis gerak lain (osilasi dawai, roda keseimbangan arloji, atom dalam molekul, dan sebagainya) yang mirip dengan jenis gerakan ini, sehingga pada kesempatan ini kita akan membahasnya secara mendetail.
Dalam kehidupan sehari-hari, gerak bolak balik benda yang bergetar terjadi tidak tepat sama karena pengaruh gaya gesekan. Ketikakita memainkan gitar, senar gitar tersebut akan berhenti bergetar apabila kita menghentikan petikan. Demikian juga bandul yang berhenti berayun jika tidak digerakan secara berulang. Hal ini disebabkan karena adanya gaya gesekan. Gaya gesekan menyebabkan benda-benda tersebut berhenti berosilasi. Jenis getaran seperti ini disebut getaran harmonik teredam. Walaupunkita tidak dapat menghindari gesekan, kita dapat meniadakan efek redaman dengan menambahkan energi ke dalam sistem yang berosilasi untuk mengisi kembali energi yang hilang akibat gesekan, salahsatu contohnya adalah pegas dalam arloji yang sering kita pakai. Pada kesempatan ini kita hanya membahas gerak harmonik sederhana secara mendetail, karena dalam kehidupan sehari-hari terdapat banyak jenis gerak yang menyerupai sistem ini.
Gerak harmonis sederhana yang dapat dijumpai dalam kehidupan sehari-hari adalah getaran benda pada pegas dan getaran benda pada ayunan sederhana.Kita akan mempelajarinya satu persatu.
Gerak Harmonis Sederhana pada Ayunan
 Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam di titik kesetimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.
Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam di titik kesetimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan beban akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.
Besaran fisika pada Gerak Harmonik Sederhana pada ayunan sederhana
Benda yang bergerak harmonis sederhana pada ayunan sederhana memiliki periode alias waktu yang dibutuhkan benda untuk melakukan satu getaran secara lengkap. Benda melakukan getaran secara lengkap apabila benda mulai bergerak dari titik di mana benda tersebut dilepaskan dan kembali lagi ke titik tersebut.
Pada contoh di atas, benda mulai bergerak dari titik A lalu ke titik B, titik C dan kembali lagi ke B dan A. Urutannya adalah A-B-C-B-A. Seandainya benda dilepaskan dari titik C maka urutan gerakannya adalah C-B-A-B-C.
Jadi periode ayunan (T) adalah waktu yang diperlukan benda untuk melakukan satu getaran (disebut satu getaran jika benda bergerak dari titik di mana benda tersebut mulai bergerak dan kembali lagi ke titik tersebut ). Satuan periode adalah sekon atau detik.
Selain periode, terdapat juga frekuensi alias banyaknya getaran yang dilakukan oleh benda selama satu detik. Yang dimaksudkan dengan getaran di sini adalah getaran lengkap. Satuan frekuensi adalah 1/sekon atau s-1. 1/sekon atau s-1 disebut juga hertz, menghargai seorang fisikawan. Hertz adalah nama seorang fisikawan tempo doeloe. Silahkan baca biografinya untuk mengenal almahrum eyang Hertz lebih dekat.
Hubungan antara Periode dan Frekuensi
Frekuensi adalah banyaknya getaran yang terjadi selama satu detik/sekon. Dengan demikian selang waktu yang dibutuhkan untuk melakukan satu getaran adalah :![]()
Selang waktu yang dibutuhkan untuk melakukan satu getaran adalah periode. Dengan demikian, secara matematis hubungan antara periode dan frekuensi adalah sebagai berikut :

Amplitudo (f)
Pada ayunan sederhana, selain periode dan frekuensi, terdapat juga amplitudo. Amplitudo adalah perpindahan maksimum dari titik kesetimbangan. Pada contoh ayunan sederhana sesuai dengan gambar di atas, amplitudo getaran adalah jarak AB atau BC.
Gerak Harmonis Sederhana pada Pegas
 Semua pegas memiliki panjang alami sebagaimana tampak pada gambar a. Ketika sebuah benda dihubungkan ke ujung sebuah pegas, maka pegas akan meregang (bertambah panjang) sejauh y. Pegas akan mencapai titik kesetimbangan jika tidak diberikan gaya luar (ditarik atau digoyang), sebagaimana tampak pada gambar B. Jika beban ditarik ke bawah sejauh y1 dan dilepaskan (gambar c), benda akan akan bergerak ke B, ke D lalu kembali ke B dan C. Gerakannya terjadi secara berulang dan periodik. Sekarang marikita tinjau hubungan antara gaya dan simpangan yang dialami pegas.
Semua pegas memiliki panjang alami sebagaimana tampak pada gambar a. Ketika sebuah benda dihubungkan ke ujung sebuah pegas, maka pegas akan meregang (bertambah panjang) sejauh y. Pegas akan mencapai titik kesetimbangan jika tidak diberikan gaya luar (ditarik atau digoyang), sebagaimana tampak pada gambar B. Jika beban ditarik ke bawah sejauh y1 dan dilepaskan (gambar c), benda akan akan bergerak ke B, ke D lalu kembali ke B dan C. Gerakannya terjadi secara berulang dan periodik. Sekarang marikita tinjau hubungan antara gaya dan simpangan yang dialami pegas.
Kita tinjau pegas yang dipasang horisontal, di mana pada ujung pegas tersebut dikaitkan sebuah benda bermassa m. Massa benda kita abaikan, demikian juga dengan gaya gesekan, sehingga benda meluncur pada permukaan horisontal tanpa hambatan. Terlebih dahulu kita tetapkan arah positif ke kanan dan arah negatif ke kiri. Setiap pegas memiliki panjang alami, jika pada pegas tersebut tidak diberikan gaya. Pada kedaan ini, benda yang dikaitkan pada ujung pegas berada dalam posisi setimbang (lihat gambar a). Untuk semakin memudahkan pemahaman dirimu,sebaiknya dilakukanjuga percobaan.
 Apabila benda ditarik ke kanan sejauh +x (pegas diregangkan), pegas akan memberikan gaya pemulih pada benda tersebut yang arahnya ke kiri sehingga benda kembali ke posisi setimbangnya (gambar b).
Apabila benda ditarik ke kanan sejauh +x (pegas diregangkan), pegas akan memberikan gaya pemulih pada benda tersebut yang arahnya ke kiri sehingga benda kembali ke posisi setimbangnya (gambar b).
 Sebaliknya, jika benda ditarik ke kiri sejauh -x, pegas juga memberikan gaya pemulih untuk mengembalikan benda tersebut ke kanan sehingga benda kembali ke posisi setimbang (gambar c).
Sebaliknya, jika benda ditarik ke kiri sejauh -x, pegas juga memberikan gaya pemulih untuk mengembalikan benda tersebut ke kanan sehingga benda kembali ke posisi setimbang (gambar c). Besar gaya pemulih F ternyata berbanding lurus dengan simpangan x dari pegas yang direntangkan atau ditekan dari posisi setimbang (posisi setimbang ketika x = 0). Secara matematis ditulis :
Besar gaya pemulih F ternyata berbanding lurus dengan simpangan x dari pegas yang direntangkan atau ditekan dari posisi setimbang (posisi setimbang ketika x = 0). Secara matematis ditulis :
F = -kx
Persamaan ini sering dikenal sebagai hukum hooke dan dicetuskan oleh paman Robert Hooke. k adalah konstanta dan x adalah simpangan. Hukum Hooke akurat jika pegas tidak ditekan sampai kumparan pegas bersentuhan atau diregangkan sampai batas elastisitas. Tanda negatif menunjukkan bahwa gaya pemulih alias F mempunyai arah berlawanan dengan simpangan x. Ketikakita menarik pegas ke kanan maka x bernilai positif, tetapi arah F ke kiri (berlawanan arah dengan simpangan x). Sebaliknya jika pegas ditekan, x berarah ke kiri (negatif), sedangkan gaya F bekerja ke kanan. Jadi gaya F selalu bekeja berlawanan arah dengan arah simpangan x. k adalah konstanta pegas. Konstanta pegas berkaitan dengan kaku atau lembut sebuah pegas. Semakin besar konstanta pegas (semakin kaku sebuah pegas), semakin besar gaya yang diperlukan untuk menekan atau meregangkan pegas. Sebaliknya semakin lembut sebuah pegas (semakin kecil konstanta pegas), semakin kecil gaya yang diperlukan untuk meregangkan pegas. Untuk meregangkan pegas sejauh x,kita akan memberikan gaya luar pada pegas, yang besarnya sama dengan F = +kx. Pegas dapat bergerak jika terlebih dahulu diberikan gaya luar. Amati bahwa besarnya gaya bergantungjuga pada besar x (simpangan).
Sekarang mari kita tinjau lebih jauh apa yang terjadi jika pegas diregangkan sampai jarak x = A, kemudian dilepaskan (lihat gambar di bawah).
 Setelah pegas diregangkan, pegas menarik benda kembali ke posisi setimbang (x=0). Ketika melewati posisi setimbang, benda bergerak dengan laju yang tinggi karena telah diberi percepatan oleh gaya pemulih pegas. Ketika bergerak pada posisi setimbang, gaya pegas = 0, tetapi laju benda maksimum.
Setelah pegas diregangkan, pegas menarik benda kembali ke posisi setimbang (x=0). Ketika melewati posisi setimbang, benda bergerak dengan laju yang tinggi karena telah diberi percepatan oleh gaya pemulih pegas. Ketika bergerak pada posisi setimbang, gaya pegas = 0, tetapi laju benda maksimum. Karena laju benda maksimum maka benda terus bergerak ke kiri. Gaya pemulih pegas kembali memperlambat gerakan benda sehingga laju benda perlahan-lahan menurun dan benda berhenti sejenak ketika berada pada x = -A. Pada titik ini, laju benda = 0, tetapi gaya pegas bernilai maksimum, di mana arahnya menuju ke kanan (menuju posisi setimbang).
Karena laju benda maksimum maka benda terus bergerak ke kiri. Gaya pemulih pegas kembali memperlambat gerakan benda sehingga laju benda perlahan-lahan menurun dan benda berhenti sejenak ketika berada pada x = -A. Pada titik ini, laju benda = 0, tetapi gaya pegas bernilai maksimum, di mana arahnya menuju ke kanan (menuju posisi setimbang).
 Benda tersebut bergerak kembali ke kanan menuju titik setimbang karena ditarik oleh gaya pemulih pegas tadi. Gerakan benda ke kanan dan ke kiri berulang secara periodik dan simetris antara x = A dan x = -A.
Benda tersebut bergerak kembali ke kanan menuju titik setimbang karena ditarik oleh gaya pemulih pegas tadi. Gerakan benda ke kanan dan ke kiri berulang secara periodik dan simetris antara x = A dan x = -A.

Besaran fisika pada Gerak Harmonik Sederhana pada pegas pada dasarnya sama dengan ayunan sederhana, yakni terdapat periode, frekuensi dan amplitudo. Jarak x dari posisi setimbang disebut simpangan. Simpangan maksimum alias jarak terbesar dari titik setimbang disebut amplitudo (A). Satu getaran Gerak Harmonik Sederhana pada pegas adalah gerak bolak balik lengkap dari titik awal dan kembali ke titik yang sama. Misalnya jika benda diregangkan ke kanan, maka benda bergerak mulai dari titik x = 0, menuju titik x = A, kembali lagi ke titik x = 0, lalu bergerak menuju titik x = -A dan kembali ke titik x = 0 (bingung-kah ? ![]() ). Dipahami perlahan-lahan ya…
). Dipahami perlahan-lahan ya…
Bagaimana osilasi pada pegas yang digantungkan secara vertikal ?
Pada dasarnya osilasi alias getaran dari pegas yang digantungkan secara vertikal sama dengan getaran pegas yang diletakan horisontal. Bedanya, pegas yang digantungkan secara vertikal lebih panjang karena pengaruh gravitasi yang bekerja pada benda. Mari kita tinjau lebih jauh getaran pada pegas yang digantungkan secara vertikal…
 Pada pegas yang kita letakan horisontal (mendatar), posisi benda disesuaikan dengan panjang pegas alami. Pegas akan meregang atau mengerut jika diberikan gaya luar (ditarik atau ditekan). Nah, pada pegas yang digantungkan vertikal, gravitasi bekerja pada benda bermassa yang dikaitkan pada ujung pegas. Akibatnya, walaupun tidak ditarik ke bawah, pegas dengan sendirinya meregang sejauh x0. Pada keadaan ini benda yang digantungkan pada pegas berada pada posisi setimbang.
Pada pegas yang kita letakan horisontal (mendatar), posisi benda disesuaikan dengan panjang pegas alami. Pegas akan meregang atau mengerut jika diberikan gaya luar (ditarik atau ditekan). Nah, pada pegas yang digantungkan vertikal, gravitasi bekerja pada benda bermassa yang dikaitkan pada ujung pegas. Akibatnya, walaupun tidak ditarik ke bawah, pegas dengan sendirinya meregang sejauh x0. Pada keadaan ini benda yang digantungkan pada pegas berada pada posisi setimbang.
Berdasarkan hukum II Newton, benda berada dalam keadaan setimbang jika gaya total = 0. Gaya yang bekerja pada benda yang digantung adalah gaya pegas (F0 = -kx0) yang arahnya ke atas dan gaya berat (w = mg) yang arahnya ke bawah. Total kedua gaya ini sama dengan nol.
Gurumuda tetap menggunakan lambang x agar anda bisa membandingkan dengan pegas yang diletakan horisontal. Dirimu dapat menggantikan x dengan y. Resultan gaya yang bekerja pada titik kesetimbangan = 0. Hal ini berarti benda diam alias tidak bergerak.
Jika kita meregangkan pegas (menarik pegas ke bawah) sejauh x, maka pada keadaan ini bekerja gaya pegas yang nilainya lebih besar dari pada gaya berat, sehingga benda tidak lagi berada pada keadaan setimbang (perhatikan gambar c di bawah). Total kedua gaya ini tidak sama dengan nol karena terdapat pertambahan jarak sejauh x; sehingga gaya pegas bernilai lebih besar dari gaya berat. Karena terdapat gaya pegas (gaya pemulih) yang berarah ke atas maka benda akan bergerak ke atas menuju titik setimbang. (sambil lihat gambar di bawah ya).
Total kedua gaya ini tidak sama dengan nol karena terdapat pertambahan jarak sejauh x; sehingga gaya pegas bernilai lebih besar dari gaya berat. Karena terdapat gaya pegas (gaya pemulih) yang berarah ke atas maka benda akan bergerak ke atas menuju titik setimbang. (sambil lihat gambar di bawah ya). Pada titik setimbang, besar gaya total = 0, tetapi laju gerak benda bernilai maksimum (v maks), sehingga benda bergerak terus ke atas sejauh -x. Laju gerak benda perlahan-lahan menurun, sedangkan besar gaya pemulih meningkat dan mencapai nilai maksimum pada jarak -x. Setelah mencapai jarak -x, gaya pemulih pegas menggerakan benda kembali lagi ke posisi setimbang (lihat gambar di bawah). Demikian seterusnya. Benda akan bergerak ke bawah dan ke atas secara periodik. Dalam kenyataannya, pada suatu saat tertentu pegas tersebut berhenti bergerak karena adanya gaya gesekan udara.
Pada titik setimbang, besar gaya total = 0, tetapi laju gerak benda bernilai maksimum (v maks), sehingga benda bergerak terus ke atas sejauh -x. Laju gerak benda perlahan-lahan menurun, sedangkan besar gaya pemulih meningkat dan mencapai nilai maksimum pada jarak -x. Setelah mencapai jarak -x, gaya pemulih pegas menggerakan benda kembali lagi ke posisi setimbang (lihat gambar di bawah). Demikian seterusnya. Benda akan bergerak ke bawah dan ke atas secara periodik. Dalam kenyataannya, pada suatu saat tertentu pegas tersebut berhenti bergerak karena adanya gaya gesekan udara. Semua benda yang bergetar di mana gaya pemulih F berbanding lurus dengan negatif simpangan (F = -kx), maka benda tersebut dikatakan melakukan gerak harmonik sederhana (GHS) atau Osilasi Harmonik Sederhana (OHS).
Semua benda yang bergetar di mana gaya pemulih F berbanding lurus dengan negatif simpangan (F = -kx), maka benda tersebut dikatakan melakukan gerak harmonik sederhana (GHS) atau Osilasi Harmonik Sederhana (OHS).